Manual Design Of One Way Slab

In this blog you will learn about Design of one way slab of first floor of G + 5 building procedure using I.S. 456:2000. Learn Complete Structural Engineering Industry Requirements Practically With Our Daily Blogs Series

Given:-

1) Grade of Concrete = M20
2) Grade of Steel = Fe500
3) Clear Cover to Reinforcement (c) = 20 mm
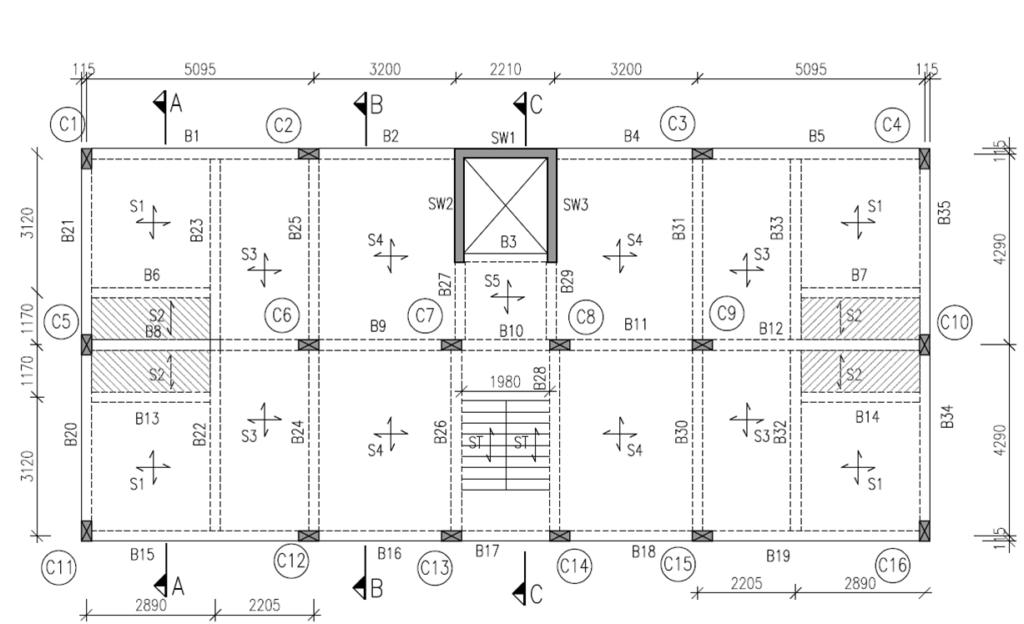
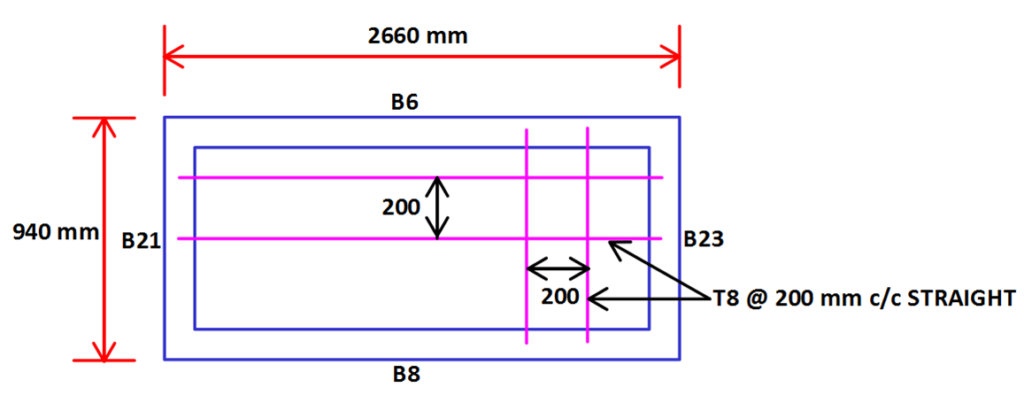
4) Dimension of Slab =  (940mm X 2660 mm)
5) Assume Beam Support (Bearing) = 230 mm
6) Unit Weight of Concrete = 25 kN/m²

Step 1 :-Aspect Ratio

(Refer Cl. No. D-1.11, Page No. 90 , I.S. 456:2000)
Lx = 940 mm & Ly = 2660 mm  …(Given)
Therefore, Ly/Lx = 2660/940 = 2.82 > 2   …(One Way Slab)

Step 2 :-Trial Depth of Slab (D)

Basic Value (B.V.) = L / D = 20
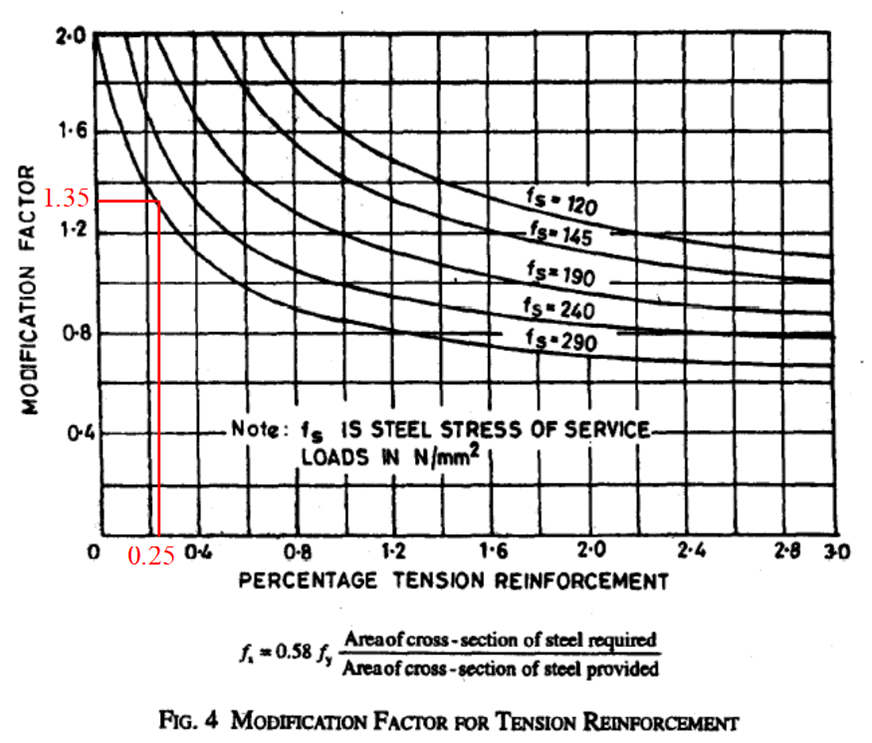
Assume % of Steel = 0.25 %
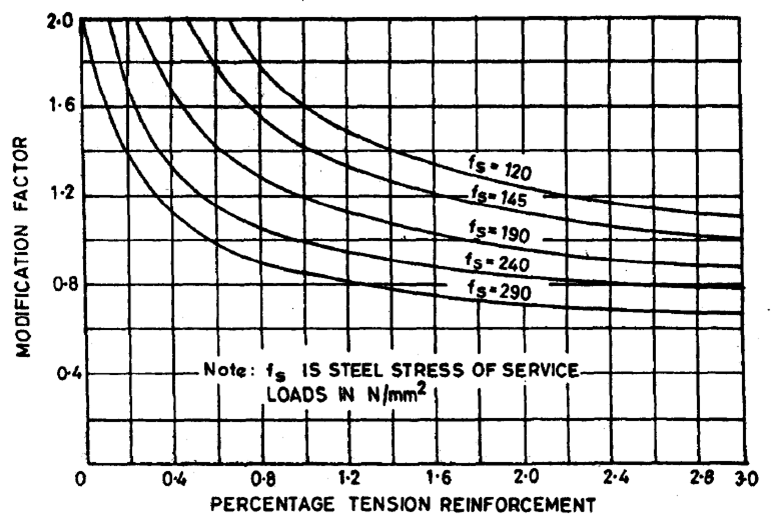
Therefore, Modification Factor (M.F.) = 1.35 …(Refer Fig. 4 , Page No. 38 I.S.456:2000)
Therefore, Effective Depth (d) = SPAN/B.V.X.N.F. =  [940/ (20 X 1.35)] = 34.81 mm
Assume Bars to be Provided of Diameter = 8 mm & Provide Clear Cover to Reinforcement = 20 mm

Therefore, Overall Depth of Slab (D) = d + c + (8/2) = 34.81 + 20 + 4 = 58.81 mm
Assume , Overall Depth of Slab (D)  = 125 mm
Therefore, Effective Depth Provided (d_provided) = D – c – (8/2) = 125 – 20 – 4 = 101 mm

Step 3 :-Effective Span (l_e)

               Minimum of,       i) Le = Lx + Bearing = 940 + 230 = 1170 mm
                                          ii) Le = Lx + d = 940 + 101 = 1041 mm

               Therefore,  Effective Span (Le) = 1041 mm

Step 4 :- Load Calculations

Consider 1 m Strip of Slab,
i) Self Weight of Slab (DL) = D X Unit Weight of Concrete
                                             = 0.125 X 25
                                             = 3.125 kN/m²
ii) Live Load (LL) = 2 kN/m²  …[Refer Table No. 1 , Page No. 7, I.S. 875  (Part 2) : 1987]
iii) Super Imposed Dead Load (SIDL) =
Floor Finish = Wt. of Screeding (50 mm Thk.) + Flooring (10 mm Thk.) + Sunk  Load(325 mm Thk.)
                     = (0.05 X 24) + (0.01 X 22) + (0.325 X 20)…[Refer I.S. 875 (Part 1) :1987]
                     = 7.92 kN/m²
                     ≈ 8 kN/m²
Total Load (W) = 3.125 + 2 + 8
                          = 13.125 kN/m²
Total Ultimate Load (Wu) = 13.125X 1.5 ≈ 19.7 kN/m²

Step 5 :- Maximum Design Bending Moment (M_umax)

Refer Table No. 26, Page No. 90 , I.S. 456:2000

Span Moment :-

M_umax= W_u . l_e² / 8
M_umax = 19.7 X  1.041² / 8 
M_umax =  2.668 kN.m
Therefore ,M_umax= 2.668 kN.m

Step 6 :- Check For Depth

              Equate   M_umax & M_ulim,
              M_umax =  M_ulim
               2.668 X 10⁶ = 0.133 X f_ck X b X d_req²
               2.668 X 10⁶ = 0.133 X 20 X 1000 X d_req²
d_req= 31.67 mm  < 101mm   …(d_req< d_provided)
              Therefore,  Safe

Step 7 :- Area of Steel Calculation :-

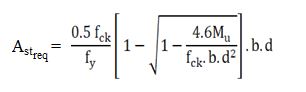
Spacing of Bars :-

As per Cl. No. 26.3.3 (b) , Page No. 46 , I.S. 456 : 2000
Maximum Spacing
Between Bars          < Minimum of   i) 3d
                                                          ii) 300 mm

Therefore,
Maximum Spacing Between Bars = i) 3 X 101 = 303 mm
                                                         ii) 300 mm
Note:- Generally We Provide 200 mm Maximum Spacing Between Bars.

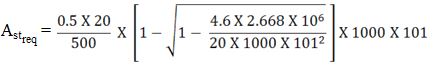
        = 61.7 mm²
Spacing of Bars = (Area of One Bar / Area of Steel) . 1000
Consider Bars to Provide are of Diameter 8mm.
Therefore, Spacing of Bars = [(π/4) X 8² / 61.7] X 1000 = 814.78 mm
Note:- Generally We Provide 200 mm Maximum Spacing Between Bars.

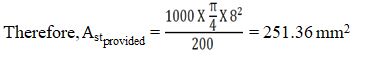
Therefore, Provide 8 mm Diameter Bars at 200 mm c/c.

Step 8 :- Distribution Steel Calculation :-

D_st = 0.12 % of the Gross Area of Slab     …(For Fe500)
Therefore, D_st= (0.12/100) X A_g
                  D_st= (0.12/100) . b . D  …(Where, b = 1000 mm &
                                                      D = Overall Depth of Slab)
                  D_st= (0.12/100) X 1000 X 125
                       = 150 mm²
Spacing of Bars = (Area of One Bar / Area of Steel) . 1000
Consider Bars to be Provide are of Diameter 8 mm.
Therefore, Spacing of Bars = [(π/4) X 8² / 150] X 1000 = 335.15 mm
Maximum Spacing
Between Bars          < Minimum of   i) 5d  = 5 X 101 = 505 mm
                                                          ii) 450 mm
Note:- Generally We Provide 200 mm Maximum Spacing Between Bars.

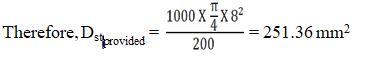
Therefore, Provide 8 mm Diameter Bars at 200 mm c/c.

Step 9 :- Check For Deflection :-

% of Steel = P_t = 100. A_streq / b.d
Therefore, P_t = (100 X 61.7) / (1000 X 101) = 0.061 %

Therefore,  F_s = 0.58 X 500 X (61.7 / 251.36) = 71.18  N/mm²
% of Steel Provided = P_t = 100. A_stprovided  / b.d
Therefore , P_t = (100 X 251.36) / (1000 X 101) = 0.248 %
M.F. = 2.0

   As, d_req < d_provided    …Safe for Deflection.

REINFORCEMENT DETAILS :-