Manual Design Of Footing Of G+5 Building Using I.S. 456:2000

In this blog you will learn Manual Design Of Footing of G+5 Building Using I.S. 456:2000 with the help of example.
Step by step guid to clear concept
Learn Complete Structural Engineering Indusry Requirements Practically With Our Daily Blogs Series

Given:

1. Grade of Concrete = M20
2. Grade of Steel = Fe500
3. Clear Cover to Reinforcement (c) = 50 mm
4. Column Dimension = 300 X 600 mm
5. Net Soil Bearing Capacity (S.B.C.) = 300  kN/m²
6. Assume Axial Load (P) from Column to Footing = 1500 kN

Load Calculation (Step 1):

Load From Column      = 1500 kN
Self Weight of Footing = Assume 10% of the column load
                                     = (10/100) X 1500
                                     = 150 kN
  ———————————————————–
Total Weight (W)         = 1650 kN

Area of Footing (A) (Step 2):

Area of Footing (A) = Total Weight (W) / Net Soil Bearing Capcity (S.B.C.)
= 1650 / 300
= 5.5 m2
Take Equal Projections From Both Sides,

5.5 = (0.6 + 2x) . (0.3 + 2x)
5.5 = 0.18 +1.2x + 0.6x + 4×2
5.5 = 0.18 +1.8x + 4×2
Therefore, by Solving Above Equation,
x = 0.95 m
Take Projection of 1 m on Both Side.

Therfore, Size of Footing = (0.3+ 2 X 1 ) & (0.6 + 2 X 1) = 2.3 X 2.6 m
Therefore Area of Footing Provided = 2.3 X 2.6 = 5.98 m2

Upward Soil Pressure (P_au) (Step 3):

P_au = (Factored Load of Column / Actual Area of Footing Provided)
     = 1.5 X 1500 / 5.98
P_au= 376.25 kN/m²

Bending Moment (B.M.) (Step 4):

The Critical Section for B.M. Along the Column Face as Shown in the Figure 2,

From X-axis:

     = (2.6 – 0.6) / 2
     = 1 m
Consider  a Strip of 1m.
Therefore, M_ux = [P_au X 1 X (C_x²/2)]
                         = [376.25 X 1 X (1² /2)]
                 M_ux = 188.125  kN.m

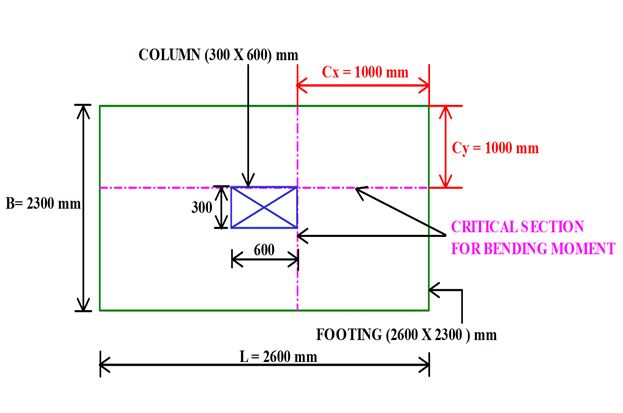
From Y-axis:

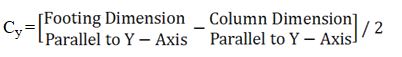
     = (2.3 – 0.3) / 2
     = 1 m
Therefore, M_uy = [P_au X 1 X (C_y²/2)]
                         = [376.25 X 1 X (1² /2)]
                  M_uy = 188.125  kN.m

Depth of Footing Required (d_req) (Step 5):

Equate The Maximum Bending Moment (Max. of M_ux & M_uy) With Limiting Moment of Resistance ,
Consider a Strip of 1m.
M_umax= M_ulim
188.125 X 10⁶ = 0.133 f_ck.b.d_req²
188.125 X 10⁶ = 0.133 X 20 X 1000 X d_req²
d_req = 265.94 mm
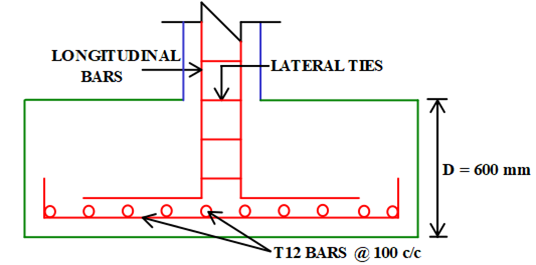
Provide 12 mm Diameter Bars at a Clear Cover of 50 mm.
Therefore, Overall Depth (D) = 265.94 + 50 + (12/2)
                                                = 321.94 mm ≈ 600 mm …(rounded -off on higher side)

Overall Depth (D) = 450 mm
Therefore, Effective Depth Provided (d_provided) =  600 – 50 – (12/2) = 544 mm

Area of Steel Calculation (A_st) (Step 6):

A_stx Along X-Direction:

A_stx = 826.8 mm²
Provide 12 mm Diameter Bars.
Spacing = (π/4 × 12² ÷ 826.8) ×100                       
= 136.8 mm ≈ 125 mm
Provide 12 mm Diameter Bars @ 125 mm c/c

A_sty Along Y-Direction:

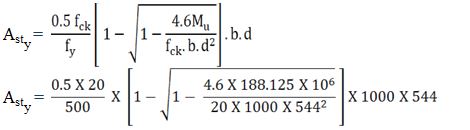
A_sty = 826.8 mm²
Provide 12 mm Diameter Bars.
Spacing = (π/4 × 12² ÷ 826.8) ×100                       
= 136.8 mm ≈ 100 mm
Provide 12 mm Diameter Bars @ 100 mm c/c

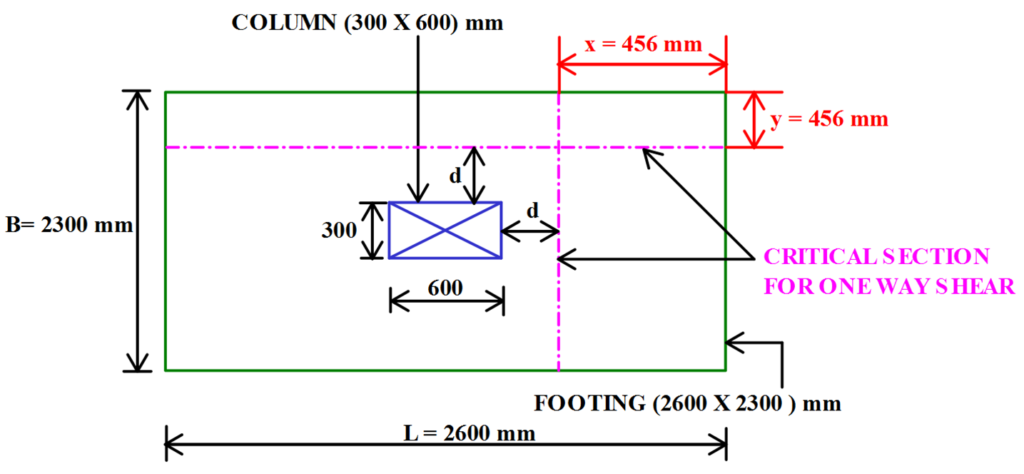
Check For One Way Shear (Step 7):

The Critical Section for One Way Shear is Taken at a Distance of ‘d’ From Column Periphery. 
The Offset x = C_x – d = 1 – 0.544 = 0.456 m
Similarly,  y = C_y – d  = 1 – 0.544 = 0.456 m
Depth of Footing at Critical Section (d’) = 544 mm

Shear Force Along X-Direction :-
V_ux = x . L . P_au = 0.456 X 1 X 376.25 = 171.57 kN

Shear Force Along Y-Direction :-
V_uy = y . B . P_au = 0.456 X 1 X 376.25 = 171.57 kN

V_umax = 209.2 kN

Nominal Shear Stress (τ_v):

τ_v  = V_umax/ b’.d’ = [(171.57 X 10³) / (1000 X 544)]  = 0.32 N/mm²

% of Steel (P_t):

P_t = 100 A_stmax / b’d’ = [(100 X 1130) / (1000 X 544)] = 0.21 %

Design Shear Stress (τ_c):

τ_c =  0.32 N/mm²  > 0.32 N/mm²
As, τ_c > τ_v    … Safe in One Way Shear

Pt	τc  ( For M20)
<0.15	0.28
0.21	?
0.25	0.36

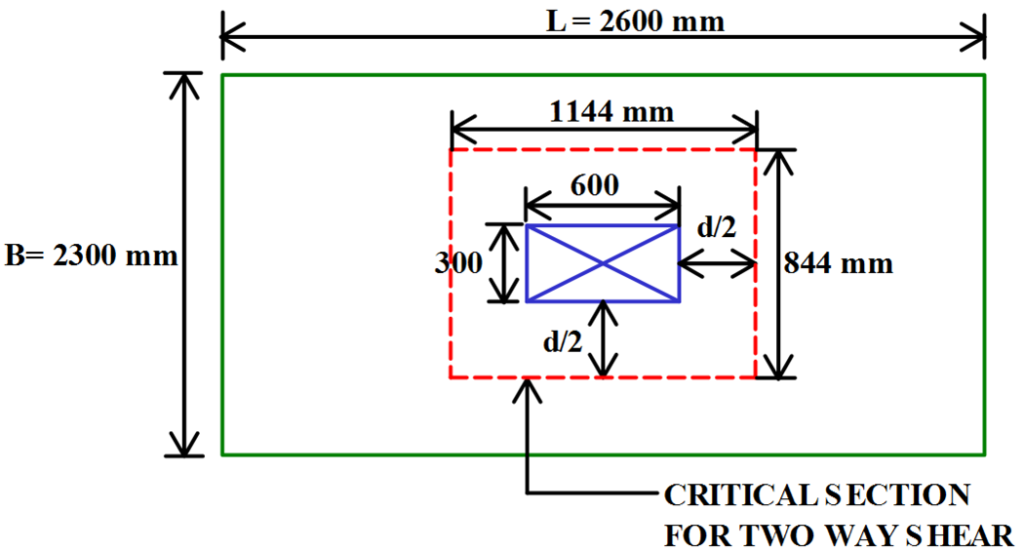
Check For Two Way Shear (Step 8):

The Critical Section for Two Way Shear is Taken at a Distance of ‘d/2’ From Column Periphery. 
Depth of Footing at Critical Section (D’) = 750 mm
Effective Depth at Critical Section = d’ = 600 – 50 – (12/2 ) = 544 mm
b’ = 2 . Perimeter of Critical Section
    = 2 X (1144 + 844)
    = 3976 mm

Shear Force on Shaded Area is Given by,
V_u = (Footing Area – Critical Section Area) . Upward Soil Pressure
V_u = [(2.6 X 2.3) – (1.144 X 0.844)] X 376.25
V_u = 1886.7 kN

Nominal Shear Stress (τ_v):

τ_v  = V_umax/ b’. d’ = [(1886.7 X 10³) / (3976 X 544)]  = 0.87 N/mm²

Design Shear Stress (τ_c’):

τ_c‘= k_s. (0.25√f_ck )
Where,  k_s= Minimum of,    i) 1
                                            ii) 0.5 + β_c = 0.5 + 0.5 = 1
                                             Where, β_c = (Breadth / Depth)_column = 300 / 600 = 0.5
Therefore, k_s= 1

Therefore,   τ_c‘= 1 X (0.25√20) = 1.118 N/mm²   >  0.87 N/mm²
As, τ_c > τ_v    … Safe in Two Way Shear