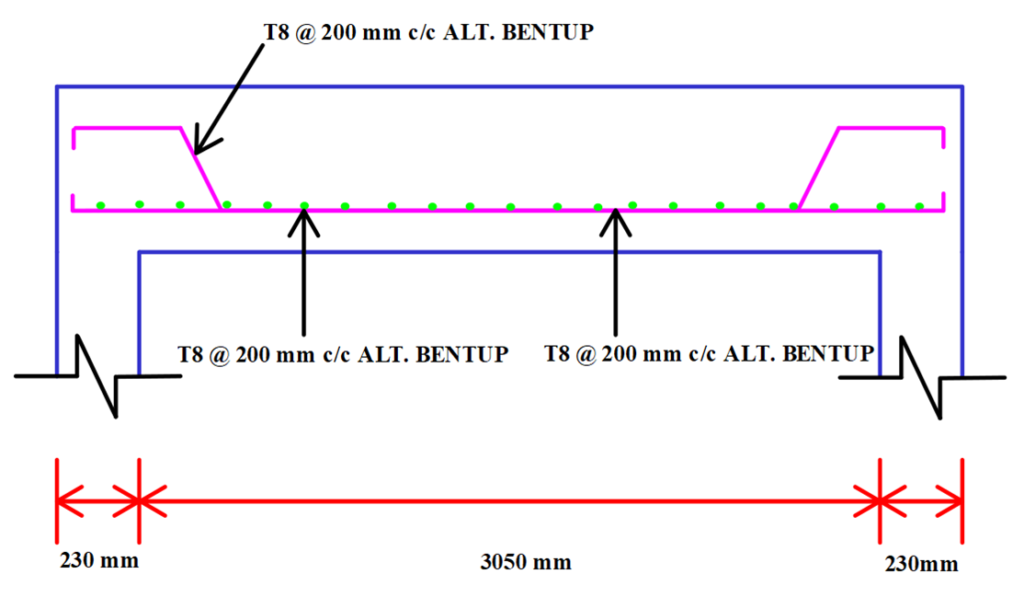
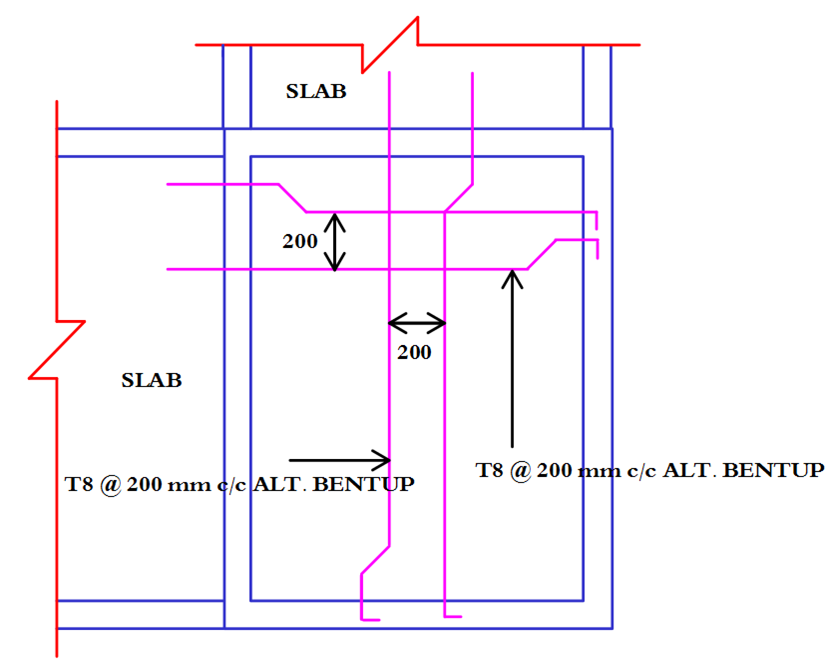
In this blog, you will learn step by step about the manual design of a two way slab for one floor of the G + 5 building procedure using I.S. 456:2000. For daily blogs, subscribe to our blog page and learn complete information about the structural engineering industry

Steps :-

Given :-

1) Grade of Concrete = M20
2) Grade of Steel = Fe500
3) Clear Cover to Reinforcement (c) = 20 mm
4) Dimension of Slab = (3050mm X 4180 mm)
5) Assume Beam Support (Bearing) = 230 mm
6) Unit Weight of Concrete = 25 kN/m²

Step 1 :- Aspect Ratio (Refer Cl. No. D-1.11, Page No. 90 , I.S. 456:2000)

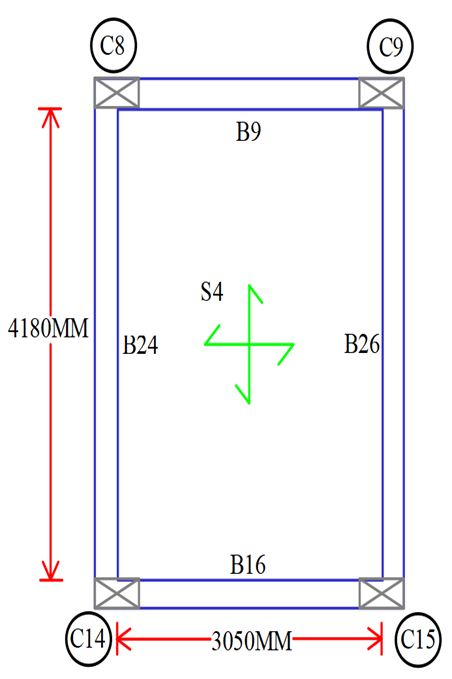
Lx = 3050 mm & Ly = 4180 mm …(Given)
Therefore, Ly/Lx = 4180/3050 = 1.37 < 2 …(Two Way Slab)

Step 2 :- Depth of Slab (D)

Basic Value (B.V.) = L / D = 26
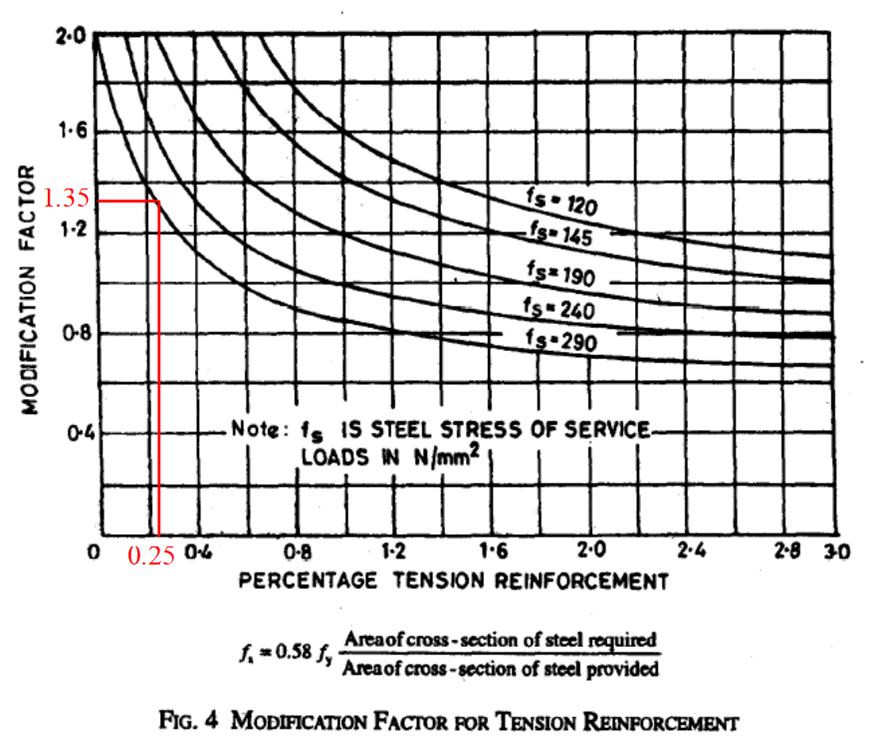
Assume % of Steel = 0.25 %
Therefore, Modification Factor (M.F.) = 1.35 …(Refer Fig. 4 , Page No. 38 , I.S.456:2000)
Therefore, Effective Depth (d) = SPAN/B.V.X.M.F = [3050 / (26 X 1.35)] = 86.894 mm

Assume Bars to be Provided of Diameter = 8 mm & Provide Clear Cover to Reinforcement = 20 mm
Therefore, Overall Depth of Slab (D) = d + c + (8/2) = 86.894 + 20 + 4 = 110.894 ≈ 125 mm
Therefore, Effective Depth Provided (d_provided) = D – c – (8/2) = 125 – 20 – 4 = 101 mm

Step 3 :- Effective Span (l_e)

               Minimum of,       i) Le = Lx + Bearing = 3050 + 230 = 3280 mm
                                         ii) Le = Lx + d = 3050 + 101 = 3151 mm
               Therefore, Effective Span (Le) = 3151 mm

Modification factor for tension reinforement | Manual design of two way slab (Fig 3)

Step 4 :- Load Calculations

Consider 1 m Strip of Slab,
i) Self Weight of Slab (DL) = D X Unit Weight of Concrete
                                             = 0.125 X 25
                                             = 3.125 kN/m²
ii) Live Load (LL)               = 2 kN/m²…[Refer Table No. 1 , Page No. 7 , I.S. 875 (Part 2) : 1987]
iii) Super Imposed Dead Load (SIDL) =
      Floor Finish = Wt. of Screeding (50 mm Thk.) + Flooring (10 mm Thk.)
                          = (0.05 X 24) + (0.01 X 22) …[Refer I.S. 875 (Part 1) : 1987]
                          = 1.42 kN/m²
                          ≈ 1.5 kN/m²

Total Load (W) = 3.125 + 2 + 1.5
                          = 6.625 kN/m²
                          ≈ 6.63 kN/m²
Total Ultimate Load (Wu) = 6.63 X 1.5
                                           = 9.945 kN/m²
                                           ≈ 9.95 kN/m²

Step 5 :- Maximum Design Bending Moment (M_umax)

	L_y/L_x
	1.3	1.37	1.4
-α_x	0.065	?	0.071
+α_x	0.049	?	0.053

Refer Table No. 26, Page No. 90 , I.S. 456:2000

Shorter Span Moments :-

1) -ve Moment at Continuous Edge :-

By Interpolation,

-α_x= 0.065+[{(0.071-0.065) / (1.4-1.3)} X (1.37 – 1.3)]
= 0.0692

M_u= -α_x . W_u . l_e²
= 0.0692 X 9.95 X 3.151²
= 6.836 kN.m

2) +ve Moment at Mid-Span :-
By Interpolation,
+α_x= 0.049+[{(0.053-0.049) / (1.4-1.3)} X (1.37 – 1.3)]
= 0.0518

M_u= +α_x . W_u . l_e²
= 0.0518 X 9.95 X 3.151²
= 5.117 kN.m

Longer Span Moments :-

3) -ve Moment at Continuous Edge :-
M_u= -α_y . W_u . l_e²
= 0.047 X 9.95 X 3.151²
= 4.64 kN.m

4) +ve Moment at Mid-Span :-
M_u= +α_y . W_u . l_e²
= 0.035 X 9.95 X 3.151²
= 3.46 kN.m

Therefore, Maximum Design Bending Moment (M_umax) = 6.836 kN.m

Step 6 :- Check For Depth

              Equate   M_umax & M_ulim,
              M_umax = M_ulim
             6.836 X 10⁶ = 0.133 X f_ck X b X d_req²
              6.836 X 10⁶ = 0.133 X 20 X 1000 X d_req²
d_req= 50.7 mm < 101 mm   …(d_req< d_provided)
              Therefore, Safe

Step 7 :- Area of Steel Calculation :-

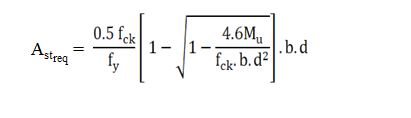
Spacing of Bars :-

As per Cl. No. 26.3.3 (b) , Page No. 46 , I.S. 456 : 2000
Maximum Spacing
Between Bars          < Minimum of   i) 3d
                                                          ii) 300 mm
Therefore,
Maximum Spacing Between Bars = i) 3 X 101 = 303 mm
                                                         ii) 300 mm

Note:- Generally We Provide 200 mm Maximum Spacing Between Bars.

Spacing of Bars = Area of one bar/ Area of steel * 1000

Along Shorter Span (L_x) :-

1) At Support :-

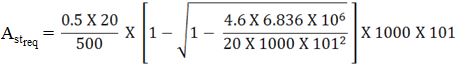
= 162.18 mm²
Spacing of Bars = (Area of One Bar / Area of Steel) . 1000
Consider Bars to Provide are of Diameter 8mm.
Therefore, Spacing of Bars = [(π/4) X 8² / 162.18] X 1000 = 3709.98 mm
Note:- Generally We Provide 200 mm Maximum Spacing Between Bars.

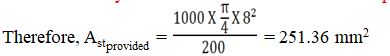
2) At Mid-Span :-

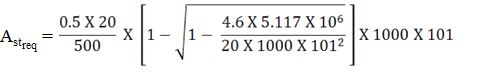
= 120.1 mm²
Spacing of Bars = (Area of One Bar / Area of Steel) . 1000
Consider Bars to be Provide are of Diameter 8mm.
Therefore, Spacing of Bars = [(π/4) X 8² / 120.1 ] X 1000 = 418.58 mm
Note:- Generally We Provide 200 mm Maximum Spacing Between Bars.

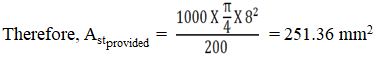
Along Longer Span (L_y) :-

d = d_provided – diameter of bar provided along shorter span = 101 – 8 = 93 mm

1) At Support :-

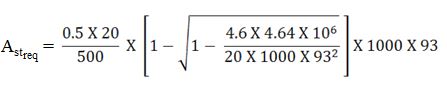
= 118.53 mm²
Spacing of Bars = (Area of One Bar / Area of Steel) . 1000
Consider Bars to be Provide are of Diameter 8mm.
Therefore, Spacing of Bars = [(π/4) X 8² / 118.53] X 1000 = 424.13mm
Note:- Generally We Provide 200 mm Maximum Spacing Between Bars.

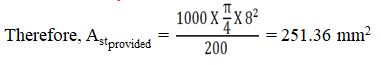
2) At Mid-Span :-

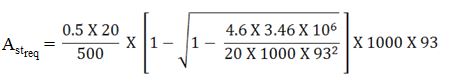
= 87.74 mm²
Spacing of Bars = (Area of One Bar / Area of Steel) . 1000
Consider Bars to be Provide are of Diameter 8mm.
Therefore, Spacing of Bars = [(π/4) X 8² / 87.74] X 1000 = 572.97 mm
Note:- Generally We Provide 200 mm Maximum Spacing Between Bars.

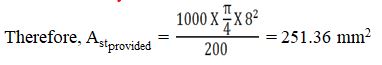
Note:- Calculation of Distribution Steel is Eliminated, Since it is a Two Way Slab.

Step 8 :- Check For Deflection :-

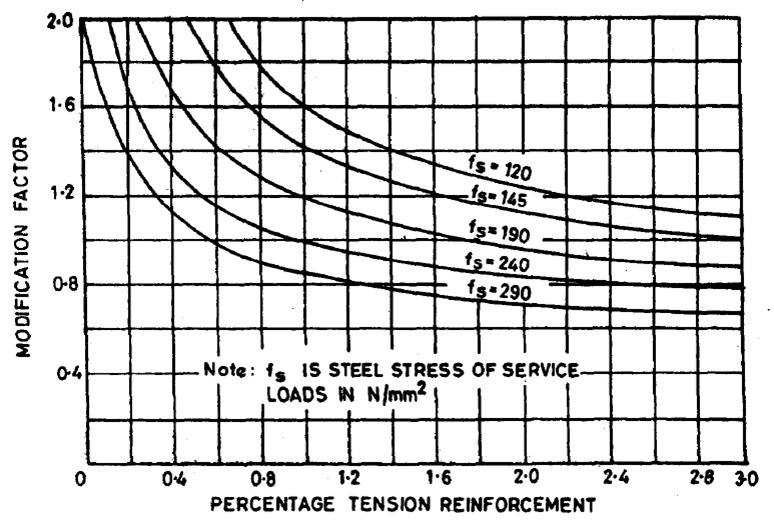
% of Steel = P_t = 100. A_streq / b.d
Therfore, P_t= (100 X 120.1) / (1000 X 101) = 0.11 %
Therefore, F_s= 0.58 X 500 X (120.1 / 251.36) = 138.56 N/mm²
% of Steel Provided = P_t = 100. A_stprovided / b.d
Therefore , P_t= (100 X 251.36) / (1000 X 101) = 0.248 %
M.F. = 2.0
Now, d_req= SPAN/B.V.X.M.F = [3151/(26 X 2)] = 60.6mm < 101 mm
As, d_req< d_provided …Safe for Deflection.