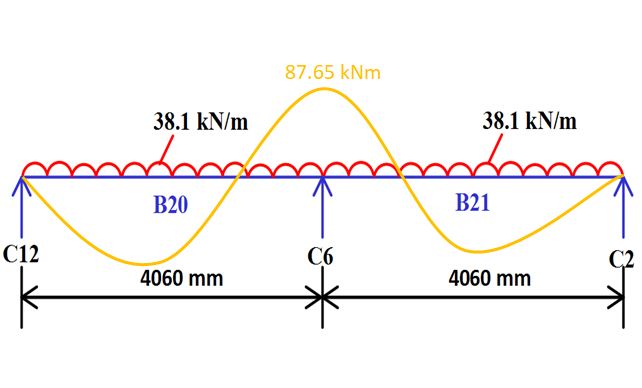
Manual Design Of Doubly Reinforced Continuous Beam
In this blog, you will learn step by step about the design of doubly reinforced beam of first floor of G+5 building procedure using I.S. 456:2000. For daily blogs, subscribe to our blog page and learn complete information about the structural engineering industry Given:- 1) Grade of Concrete = M202) Grade of Steel = Fe5003) Clear …
Manual Design Of Doubly Reinforced Continuous Beam Read More »