Manual Design Of Doubly Reinforced Continuous Beam

In this blog, you will learn step by step about the design of doubly reinforced beam of first floor of G+5 building procedure using I.S. 456:2000. For daily blogs, subscribe to our blog page and learn complete information about the structural engineering industry

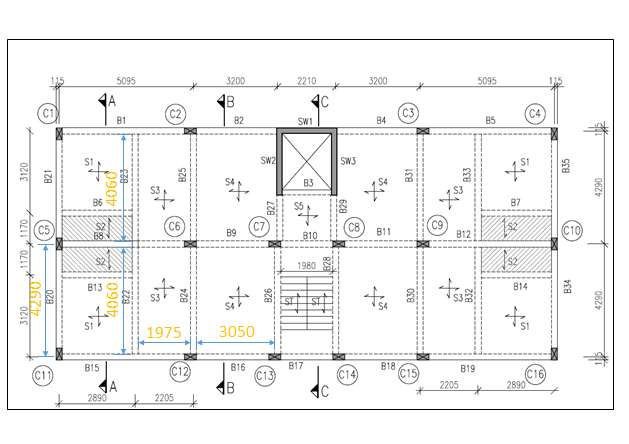
Given:-

1) Grade of Concrete = M20
2) Grade of Steel = Fe500
3) Clear Cover to Reinforcement (c) = 25 mm
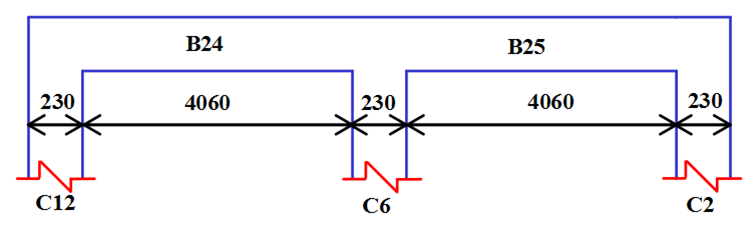
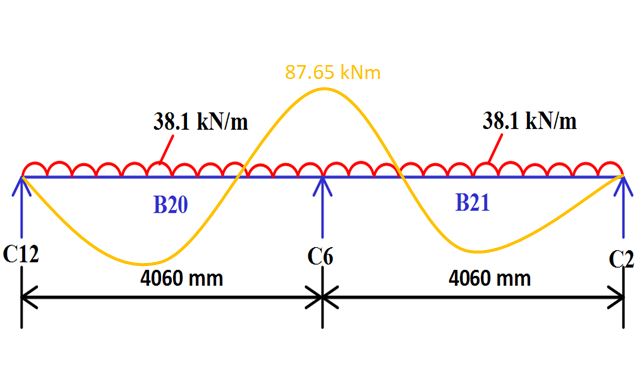
4) Length of Beam :-  B24 & B25 = 4060 mm
5) Unit Weight of Concrete = 25 kN/m²
6) Slab Dimensions :- S3 = (1975 mm X 4060 mm) & S4 = (3050 mm X 4060 mm)
7) Floor to Floor Height (H) = 3000 mm

Step 1 :- Trial Dimension of The Beam :-

Assume the Width of The Beam (b) = 230 mm
Effective Depth of Beam (d) = (L/10) to (L/15) = (4290/10) to (4290/15)
                                               = 429 mm to 286 mm
                                  Take, d = 325 mm
Assume, 20 mm Diameter Bars are to be Provided  at a Clear Cover of 25 mm.
Therefore,  Overall Depth (D) = 325 + (20/2) + 25 = 360 mm ≈ 375 mm
…(Rounded off on Higher Side)
Therefore, Effective Depth of Beam Provided (d) = 375 – (20/2) – 25 = 340 mm 

Step 2 :- Effective Span (L_e) :-

Minimum of The Following ,
 i) Le = L + d = 4060 + 340 = 4400 mm
ii) Le = L + Bearing = 4060 + 230 = 4290 mm
Therefore, Effective Span (L_e) = 4290 mm

Step 3 :- Load Calculations :-

Load on Beam B24 & B25 :-
i) Super Imposed Dead Load (SIDL) :-
Wall Load = Wall Thickness X Floor to Floor Height X Unit Weight of Bricks 
                  = (0.150 X 3 X 20) = 9 kN/m
                  …(No Deduction of Depth of Beam is Made From Floor to Floor Height)
ii) Slab Load Transferring on Beam :-
Slab S3 :-
a) Self Weight of Slab (DL) = D X Unit Weight of Concrete
                                             = 0.125 X 25
                                             = 3.125 kN/m²
b) Live Load (LL) = 2 kN/m²  …[Refer Table No. 1 , Page No. 7 , I.S. 875  (Part 2) : 1987]
c) Super Imposed Dead Load (SIDL) =
Floor Finish = Wt. of Screeding (50 mm Thk.) + Flooring (10 mm Thk.)
                     = (0.05 X 24) + (0.01 X 22)    …[Refer I.S. 875 (Part 1) : 1987]
                     = 1.42 kN/m²
                     ≈ 1.5 kN/m²
Total Load of Slab S3 (w)  = 3.125 + 2 + 1.5 = 6.625 kN/m²

Trapezoidal Load of  Slab S3 is Transferring  on Beam B24 & B25 Because S3 Slab is Two Way Slab Which is Given by,
W_S3 = [{(w. L_x)/2} X {1- (1/ 3. β²)}]       Where, β = l_y/l_x
       = {(6.625 X 1.975 ) / 2} X [1- {1/ 3 X (4.06/1.975)²}]
       = 6.02 kN/m
Slab S4 :-
a) Self Weight of Slab (DL) = D X Unit Weight of Concrete
                                             = 0.125 X 25
                                             = 3.125 kN/m²
b) Live Load (LL) = 2 kN/m²  …[Refer Table No. 1, Page No. 7, I.S. 875  (Part 2) : 1987]
c) Super Imposed Dead Load (SIDL) =
Floor Finish = Wt. of Screeding (50 mm Thk.) + Flooring (10 mm Thk.)
                    = (0.05 X 24) + (0.01 X 22)  … (Refer I.S. 875 (Part 1) : 1987)
                    = 1.42kN/m²
≈ 1.5 kN/m²
Total Load of Slab S4 (w)  = 3.125 + 2 + 1.5 = 6.625 kN/m²

Trapezoidal Load of Slab S4 is Transferring  on Beam B24 & B25 Which is Given by,
W_S4 = [{(w. L_x)/2} X {1- (1/ 3. β²)}]
       ={(6.625 X 3.05) / 2} X [1- {1/ 3 X (4.06/3.05)²}]
       = 8.2 kN/m
Therefore, Total Load of Slabs Transfers on Beam B24 & B25 = W_S1 + W_S4
                                                                                                    = 6.02 + 8.2
                                                                                                    = 14.22  kN/m
iii) Self Weight of Beam (DL) = b X D X Unit Weight of Concrete
                                                 = 0.230 X 0.375 X 25
                                                 = 2.156 kN/m

Total Load on Each Beam B24 & B25 (W) = 9 + 14.22 + 2.156 = 25.376 kN/m
                                                                                                      ≈ 25.4 kN/m
Ultimate Load (W_u) = 25.4 X 1.5 = 38.1 kN/m

Step 4 :- Bending Moment (M_u) :-

Max. Moment on Continuous
Beam (B24 & B25)  is (M) = W . L_e² / 8
                                            = (25.4 X 4.29²) / 8
                                            = 58.43 kN.m
Ultimate Moment on Continuous
Beam (B20 & B21)  is (M_u) =58.43X 1.5 = 87.65 kN.m

CONTINUOUS BEAM HAVING TWO EQUAL SPAN CARRYING UNIFORMALLY DISTRIBUTED LOAD (UDL) OVER ENTIRE SPAN :-

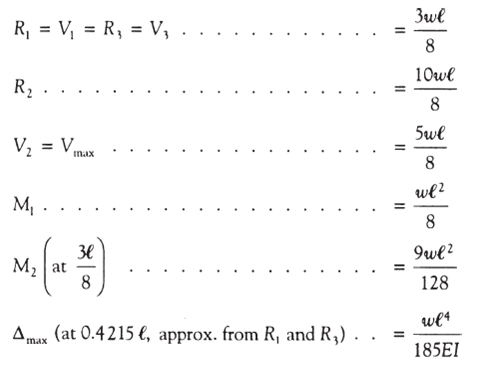
Step 5 :- Limiting Moment of Resistance :-

M_ulim= 0.133 fck.b.d²
M_ulim= 0.133 X 20 X 230 X 340²
M_ulim= 0.133 X 20 X 230 X 340²
M_ulim= 70724080 N
M_ulim= 70724080 / 10⁶
M_ulim= 70.72 kN.m
As, M_ulim<  M_u

Note :- Either We Have to Increase Depth and Design as a Singly Reinforced Beam or if We Are Not Allowed to Increase Depth of Beam Then We Will Design the Beam as a Doubly Reinforced Beam. So We Design Assumed Beam of 230 X 375 mm As Doubly Reinforced Beam.

Step 6 :- Balanced Moment (M_u2) :-

                                Equate,  M_u2 = M_u – M_ulim
M_u2 = 87.65 –  70.72
                                M_u2 = 16.93 kN.m

Step 7 :- Area of Steel Calculation (A_st) :-

[Refer Cl. No. 26.5.1.1 (a) & (b), Page No. 46 & 47,I.S. 456 : 2000]

A_stmin = As/bd = 0.85/ Fy
A_stmin= A_s = [(0.85 X 230 X 340) / 500]
A_stmin= A_s = 132.94 mm²
A_stmax = 0.04 b.D
= 0.04 X 230 X375
          = 3450 mm²

i) Steel in Tensile Zone :-
A_streq= A_st1+A_st2

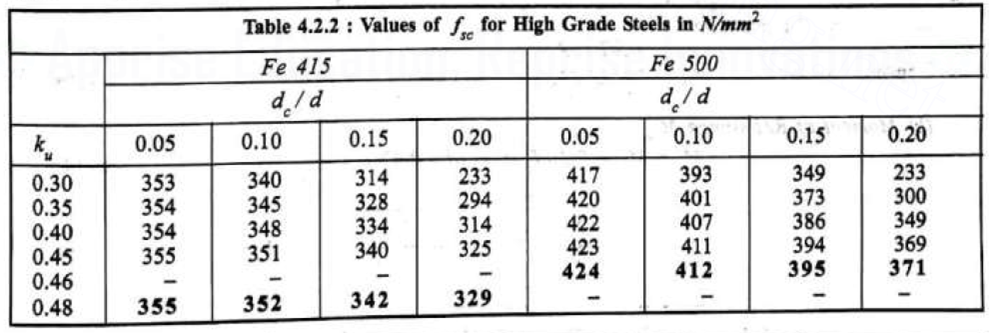
[For k_umax & f_sc Refer above Tables From, Illustrated  Design of Reinforced Concrete Buildings by S. R. Karve & V. L. Shah]

ii) Steel in Compression Zone :-
d_c / d= (D – d) / d = (375 – 340) / 340 = 0.1
By Interpolation,
f_sc = 412 N/mm²     …Refer Table 4.2.2

Step 8 :- Check For Shear :-

Codal Provisions for Shear :- [Refer Cl. No. 26.5.1.6, Page No. 48 & Cl. No. 40.1, 40.3, Page No. 72 of  I.S. 456 : 2000]

i) Maximum Shear Force (V_u) :-
V = (5.W . L_e/ 8)
     = [(5 X 25.4 X 4.29) / 8]
     = 68.1 kN
V_u= 68.1 X 1.5 = 102.15 kN

ii) Nominal Shear Stress (τ_v) :-
τ_v = V_u / b.d
    = [(102.15 X 10³) / (230 X 340)]
= 1.3 N/mm² < 2.8 N/mm² (τ_cmax)     (Refer Table 20, I.S. 456:2000)

iii) % of Steel (P_t) :-
P_t=  [(100. A_stprovided) / b.d]
Therefore , P_t = (100 X 942.6) / (230 X 340) = 1.2 %

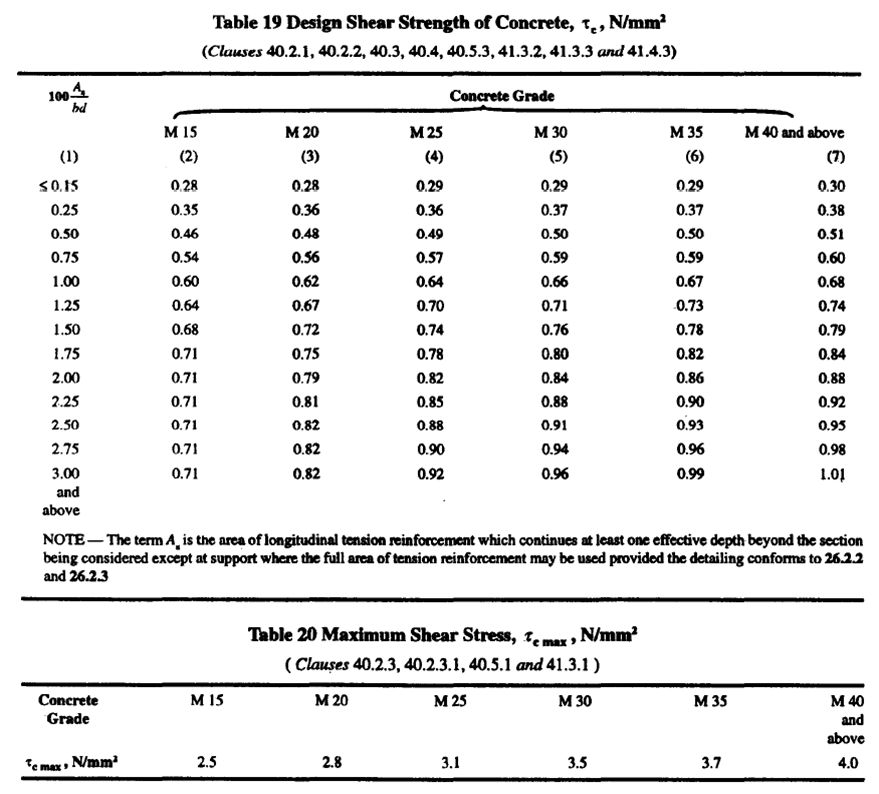
iv) Design Shear Stress (τ_c) :- (Refer Table No. 19, Page No.73, I.S. 456 : 2000) 
By Interpolation,
τ_c = [0.62 + {(0.67- 0.62) / (1.25 – 1)}X (1.2 – 1)]
    = 0.66 N/mm²  < 1.29 N/mm²
As, τ_c < τ_v
We Need to Design For Shear Reinforcement.

As per Table No. 20 , Page No. 73 , I.S. 456 : 2000
Maximum Shear Stress for M20 Grade Concrete is, τ_cmax= 2.8 N/mm²
Therefore,  Beam B20 & B21 Both Are Safe in Shear.

Step 9 :- Design of Shear Reinforcement :-

(Refer Cl. No. 40.1, Page No. 73 of  I.S. 456 : 2000]

i) Shear Resisted by Stirrups (V_us) :-
V_us= V_u – V_uc ….( For Simply Supported Beam )
      = V_u – τ_c .b.d
      = 102.15 X 10³ – 0.66 X 230 X 340
      = 50538 N
      = 50.538 kN
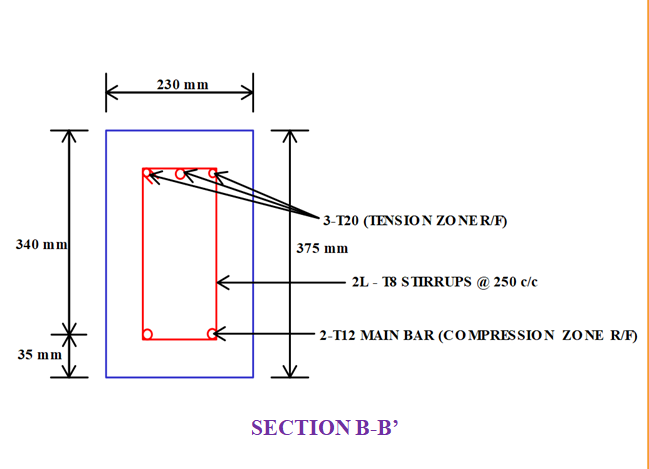
Provide 2-Legged 8mm Diameter Stirrups

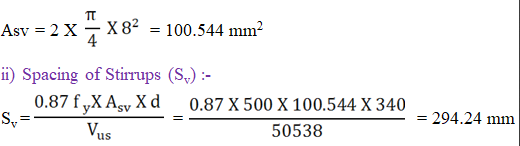
iii) Check For Stirrups Spacing :-
Spacing of Stirrups Should Not be Greater Than Minimum of The Following,
Spacing of Stirrups (S_v) = Min. of    i) 0.75d
                                                         ii) 300 mm
Therefore, Spacing of Stirrups (S_v) =  i) 0.75 X 390 = 292.5 mm < 294.24 mm Or
                                                            ii) 300 mm > 294.24 mm
Therefore, Spacing of Stirrups (S_v) = 292.5 mm ≈ 250 mm
Therefore,  Provide 2-Legged 8 mm Diameter Stirrups at a Spacing of 250 mm c/c.

Step 10 :- Check For Deflection :-

Permissible Deflection (Δ) = L_e / 350 = 4290 / 350 = 12.25 mm
For Simply Supported Beam,